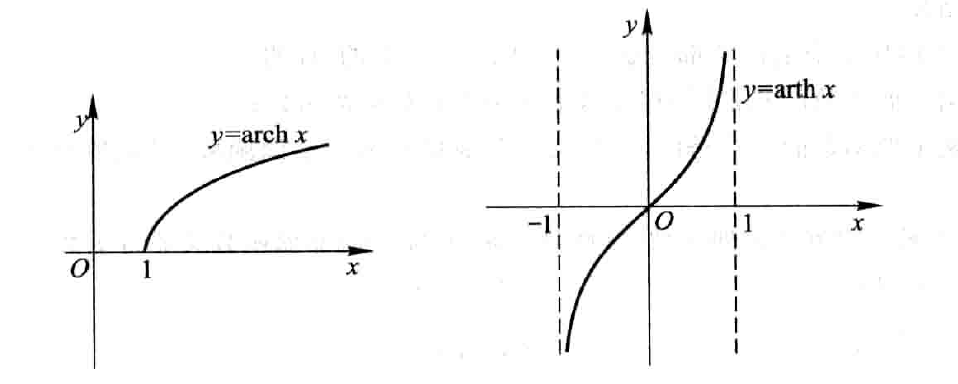摘要:《高等数学第7版上册》同济大学数学系出版读书笔记--映射与函数。
初等数学的研究对象基本是不变的量,而高等数学的研究对象则是变动的量。所谓函数关系就是变量之间的依赖关系,极限方法是研究变量的一种基本方法。
设X、Y是两个非空集合,如果存在一个法则\(f\),使得对X中每个元素\(x\),按法则\(f\),在Y中有唯一确定的语速\(y\)与之对应,那么称\(f\)为从X到Y的映射,记作:
$$f:X \to Y$$
其中\(y\)称为元素\(x\)的象,并记作\(f(x)\),即
$$y=f(x)$$
而元素\(x\)称为元素\(y\)(在映射\(f\)下)的一个原象;集合X称为映射\(f\)的定义域,记作\(D_f\),即\(D_f = X\);X中的所有元素的象所组成的集合称为映射\(f\)的值域,记作\(R_f\)或\(f(X)\),即
$$R_f = f(X)={f(x)|x \in X}$$
从映射的定义中,需要注意:
一句话概括就是,一个映射需要有定义域\(D_f\)、值域\(R_f\)和对应法则\(f\);x称为y的原象,只能一对一;y称为x的象,可以一对多。
映射又称为算子。根据集合X、Y的不同情形,在不同的数学分支中,映射又有不同的惯用名称。例如,从非空集X到数集Y的映射又称为X上的泛函,从非空集X到它自身的映射又称为X上的变换,从实数集(或其子集)X到实数集Y的映射通常称为定义在X上的函数。
设\(f\)是从集合X到集合Y的映射,若\(R_f = Y\),即Y中的任意元素y都是X中某元素的象,则称\(f\)为X到Y上的映射或满射;或对X中任意两个不同元素\(x_1 \ne x_2\),它们的象\(f(x_1) \ne f(x_2)\),则称\(f\)为X到Y的单射;若映射\(f\)即使单射,又是满射,则称\(f\)为一一映射(或双射)。
设\(f\)是X到Y的单射,则由定义,对每个\(y \in R_f\),有唯一的\(x \in X\),适合\(f(x)=y\),于是,可定义一个从\(R_f\)到X的新映射\(g\),即
$$g:R_f \to X$$
对每个\(y \in R_f\),规定\(g(y) = x\),这\(x\)满足\(f(x)=y\).这个\(g\)称为\(f\)的逆映射,记作\(f^(-1)\),其定义域\(D_(f^{-1})=R_f\),值域\(R_(f^{-1})=X\).
按上述定义,只有单射才存在逆映射。
设有两个映射
$$g:X \to Y_1, f:Y_2 \to Z $$
其中,\(Y_1 \subset Y_2\),则由映射\(g\)和\(f\)可以定出一个从X到Z的对应法则,它将每个\(x \in X\)映射成\(f[g(x)] \in Z\). 显然,这个对应法则确定了一个从X到Z的映射,这个映射称为映射\(g\)和\(f\)构成的复合映射,记作\(f \circ g\),即
$$f \circ g:X \to Z, (f \circ g)(x)=f[g(x)], x \in X$$
由复合映射的定义可知,映射\(g\)和\(f\)构成复合映射的条件是:\(g\)的值域\(R_g\)必须包含在\(f\)的定义域内,即\(R_f \subset D_f\).否则,不能构成复合映射。
复合映射具有顺序,\(f \circ g\)有意义,不代表\(g \circ f\)也有意义。
设数集\(D \subset R\),则称映射\(f: D \to R\)为定义在D上的函数,通常简记为:
$$y=f(x), x \in D$$
其中\(x\)称为自变量,\(y\)称为因变量,D称为定义域,记作\(D_f\), 即\(D_f=D\)
函数的定义中,对每个\(x \in D\),按对应法则\(f\),总有唯一确定的值\(y\)与之对应,这个值称为函数\(f\)在\(x\)处的函数值,记作\(f(x)\), 即\(y=f(x)\)。因变量\(y\)与自变量\(x\)之间的依赖关系,称为函数关系。函数值\(f(x)\)的全体所构成的集合称为函数\(f\)的值域,记作\(R_f或f(D)\),即
$$R_f=f(D)={y|y=f(x), x \in D}$$
按照上述的定义,记号\(f\)和\(f(x)\)的含义是有区别的:前者表示自变量\(x\)与因变量\(y\)之间的对应法则,而后者表示与自变量\(x\)对应的函数值。
函数是从实数集到实数集的映射,其值域总在R内,因此构成函数的要素是:定义域\(D_f\)及对应法则\(f\)。
一种是对有实际背景的函数,根据实际背景中变量的实际意义确定。比如指定的时间,从0开始还是\(t_1\)时刻开始。
一种是抽象地用算式表达式的函数,通常约定这种函数的定义域是使得算式有意义的一切实数组成的集合,这种定义域称为函数的自然定义域。比如\(y=\frac{1}{\sqrt{1-x^2}}\)的定义域为(-1.1).
表格法
图形法:\({P(x, y) | y=f(x), x \in D}\)称为函数\(y=f(x), x \in D\)的图形
解析法(公式法)
绝对值函数:
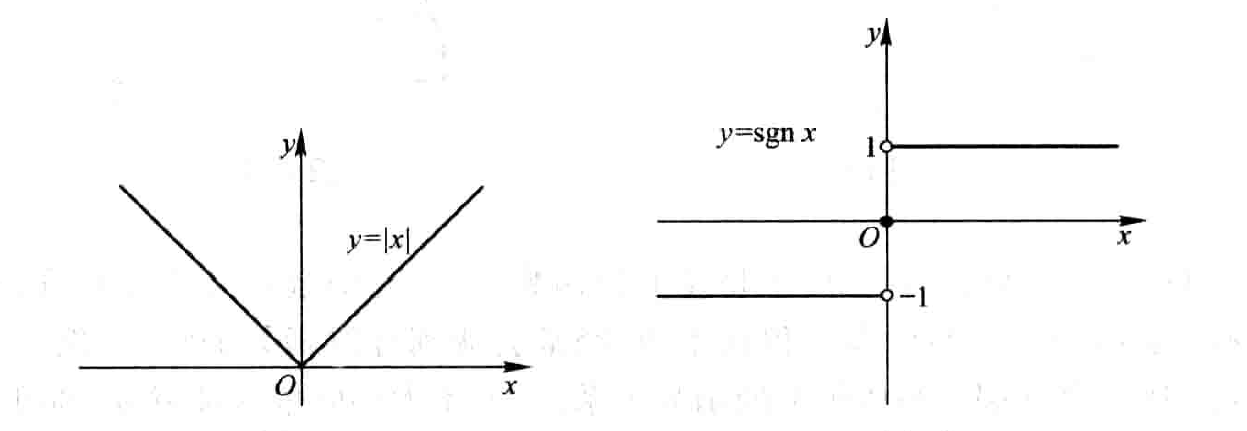
$$y=|x|=\begin{cases} -x & x < 0 \\ x & x \gt 0 \end{cases}$$
符号函数:
$$y=sgn x=\begin{cases} -1 & x < 0 \\ 0 & x=0 \\ 1 & x \gt 0 \end{cases}$$
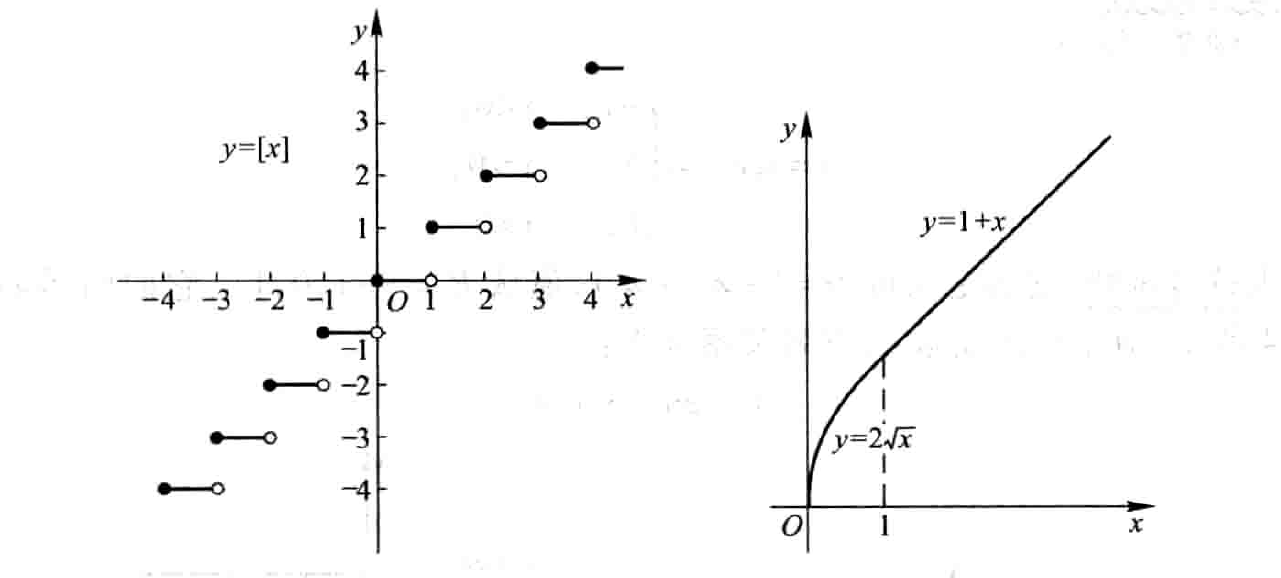
取整函数(图形称为阶梯曲线,图形发生跳跃,跃度为1):
$$[x]$$
分段函数:
$$y=f(x)=\begin{cases} 2\sqrt{x} & 0 \le x \le 1 \\ 1+x & x \gt 1 \end{cases}$$
有界性
设函数的\(f(x)\)的定义域为D,数集\(X \subset D\)。
如果存在数\(K_1\),使得
$$f(x) \le K_1$$
对任意一\(x \in X\)都成立,那么称函数\(f(x)\)在X上有上界,而\(K_1\)称为函数\(f(x)\)在X上的一个上界。
如果存在数\(K_2\),使得
$$f(x) \ge K_2$$
对任意一\(x \in X\)都成立,那么称函数\(f(x)\)在X上有下界,而\(K_2\)称为函数\(f(x)\)在X上的一个下界。
如果存在数\(M\),使得
$$|f(x)| \ge M$$
对任意一\(x \in X\)都成立,那么称函数\(f(x)\)在X上有界。如果这样的M不存在,就称\(f(x)\)在X上无界。
函数\(f(x)\)在X上有界的充分必要条件是它下X上既有上界又有下界。
单调性
设函数\(f(x)\)的定义域为D,区间\(I \subset D\).
如果对于区间I上任意两点\(x_1\)及\(x_2\),当\(x_1 \lt x_2\)时,恒有
$$f(x_1) < f(x_2)$$
那么称函数\(f(x)\)在区间I上是单调增加的;
如果对于区间I上任意两点\(x_1\)及\(x_2\),当\(x_1 \lt x_2\)时,恒有
$$f(x_1) > f(x_2)$$
那么称函数\(f(x)\)在区间I上是单调减少的;
单调增加和单调减少的函数统称为单调函数。
奇偶性
设函数\(f(x)\)的定义域D关于原点对称。
如果对于任意\(x \in D\),
$$f(-x)=f(x)$$
恒成立,那么称\(f(x)\)为偶函数。
如果对于任意\(x \in D\),
$$f(-x)=-f(x)$$
恒成立,那么称\(f(x)\)为奇函数。
函数\(y=sin x\)是奇函数,函数\(y=cos x\)是偶函数,函数\(y=sin x + cos x\)既非奇函数,也非偶函数。
偶函数的图形关于y轴对称,奇函数的图形关于原点对称。
周期性
设函数\(f(x)\)的定义域为D。如果存在一个整数l,是的对于任意一\(x \in D\)有\(x \pm l \in D\),且
$$f(x+l)=f(x)$$
恒成立,那么称\(f(x)\)为周期函数,l称为\(f(x)\)的周期。通常我们说周期函数的周期时指最小正周期。
函数\(sin x, cos x\)都是以\(2\pi\)为周期的周期函数,函数\(tan x\)是以\(\pi\)为周期的周期函数。
并非每个周期函数都有最小正周期,比如狄利克雷函数函数:
$$D(x)=\begin{cases} 1 & x \in Q \\ 0 & x \in Q^c \end{cases}$$
这是一个周期函数,任何正有理数r都是它的周期,因为不存在最小的正有理数,所以它没有最小正周期。
设函数\(f:D \to f(D)\)是单射,则它存在逆映射\(f^{-1}:f(D) \to D\),称次映射\(f^{-1}\)为函数\(f\)的反函数。
按此定义,对每个\(y \in f(D)\),有唯一的\(x \in D\),使得\(f(x)=y\),于是有
$$y^{-1}(x)=y$$
即反函数\(f^(-1)\)的对应法则是完全由函数\(f\)的对应法则所确定。
如\(y=x^3, x \in R\)是单射,所以存在反函数,其反函数为\(y=x^{\frac{1}{3}}, x \in R\)
一般地,\(y=f(x), x \in D\)的反函数集成\(y=f^{-1}(x), x \in f(D)\)
若\(f\)是定义在D上的单调函数,则\(f:D \to f(D)\)是单射,于是\(f\)的反函数\(f^{-1}\)必定存在,且容易证明\(f^{-1}\)也是\(f(D)\)上的单调函数。
反函数与原函数关于直线\(y=x\)对称
设函数\(y=f(u)\)的定义域为\(D_f\),函数\(u=g(x)\)的定义域为\(D_g\),且其值域\(R_g \subset D_f\),则由下式确定的函数
$$y=f[g(x)], x \in D_g$$
称为由函数\(u=g(x)\)与\(y=f(u)\)构成的复合函数,它的定义域为\(D_g\),变量u称为中间变量。
函数\(g\)与函数\(f\)构成的复合函数,即按“先\(g\)后\(f\)”的次序复合的函数,通常记作\(f \circ g\),即
$$(f \circ g)(x)=f[g(x)], x \in D_g$$
与复合映射一样,\(g\)与\(f\)能构成复合函数\(f \circ g\)的条件是:函数\(g\)的值域\(R_g\)必须包含于函数\(f\)的定义域\(D_f\),即\(R_g \subset D_f\)。否则,不能构成复合函数。
设函数\(f(x), g(x)\)的定义域依次为\(D_f, D_g, D=D_f \cap D_g \ne \varnothing\),则可以定义两个函数的下列运算:
和(差)\(f \pm g : (f \pm g)(x)=f(x) \pm g(x) , x \in D\)
积\(f \cdot g : (f \cdot g)(x)=f(x) \cdot g(x) , x \in D\)
商\(\frac{f}{g} : \left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)} , x \in D \) ,\(g(x) \ne 0, x \in D\)
冥函数:\(y=x^{\mu}, \mu \in R\)
指数函数:\(y=a^x, a>0且a \ne 1\)
对数函数:\(y=log_{a}^{x}, a>0且a \ne 1\),特别当\(a=e\)时,记为\(y=ln x\)
三角函数:\(y=sin x, y=cos x, y=tan x\)等
反三角函数:\(y=arcsin x, y=arccos x, y=arctan x\)等
以上五类函数统称为基本初等函数。
由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数,称为初等函数。
例如,\(y=\sqrt{1-x^2}, y=sin^{2}x, y=\sqrt{cot\frac{x}{2}}\)
以e为底的指数函数\(y=e^x\)和\(y=e^{-x}\)所产生的双曲函数以及它们的反函数--反双曲函数,定义如下:
双曲正弦:\(sh x=\frac{e^x - e^{-e}}{2}\)
双曲余弦:\(ch x=\frac{e^x + e^{-e}}{2}\)
双曲正弦:\(th x=\frac{sh x}{ch x}=\frac{e^x - e^{-e}}{e^x + e^{-e}}\)
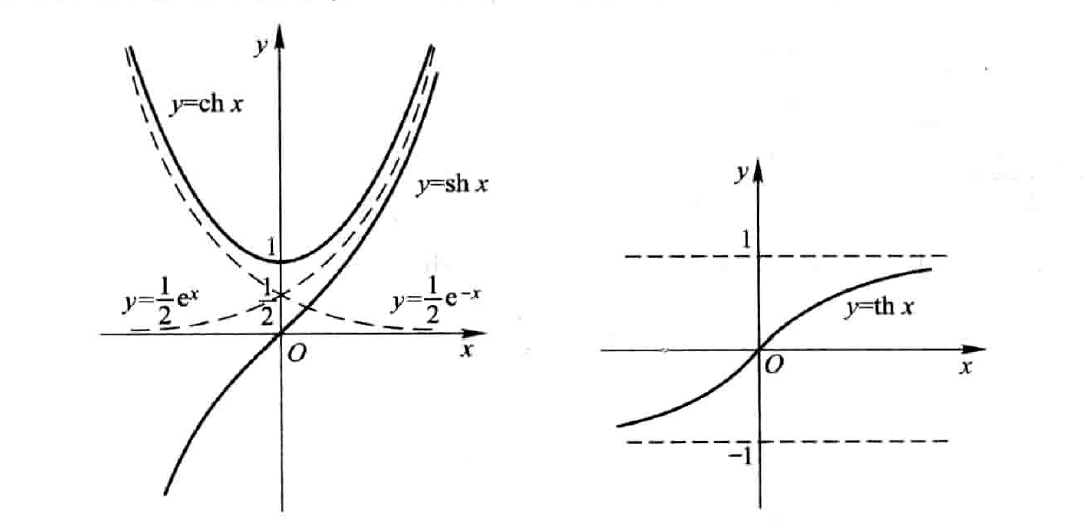
根据双曲函数的定义,可以证明下列四个公式:
\(sh(x+y)=sh x ch y + ch x sh y\) (1)
\(sh(x-y)=sh x ch y - ch x sh y\) (2)
\(ch(x+y)=ch x ch y + sh x sh y\) (3)
\(sh(x-y)=ch x ch y - sh x sh y\) (4)
由以上4个公式可以推导其他一些公式:
另(4)中的\(x=y\),并注意到ch 0=1,得:\(ch^2 x - sh^2 x =1\)
另(1)中的\(x=y\),并注意到ch 0=1,得:\(sh 2x = 2sh x ch x\)
另(3)中的\(x=y\),并注意到ch 0=1,得:\(ch 2x = ch^2 x + sh^2 x\)
双曲函数\(y=sh x, y=ch x, y=th x \)的反函数依次记为:
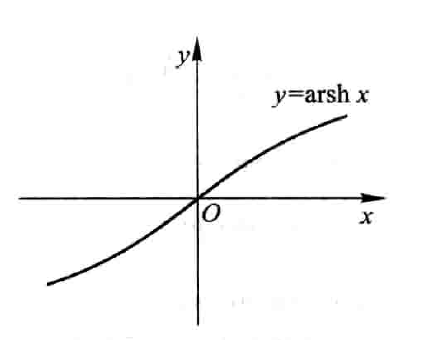
反双曲正弦:\(y=arsh x\)
反双曲余弦:\(y=arch x\)
反双曲正切:\(y=arth x\)